Polynomial arithmetic
Polynomial arithmetic includes basic mathematical operations such as addition, subtraction, and multiplication. These operations are defined naturally as if the variable  was an element of
was an element of  . Division is defined similarly, but requires that
. Division is defined similarly, but requires that  be a field. Examples of fields include rational numbers,
be a field. Examples of fields include rational numbers, 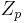 for
for  prime, and real numbers. The set of all integers is not a field and does not support polynomial division.
prime, and real numbers. The set of all integers is not a field and does not support polynomial division.
Addition and subtraction
Addition and subtraction are performed by adding or subtracting corresponding coefficients. If
then addition is defined as
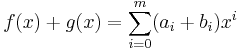 where m > n
where m > n
Multiplication
Multiplication is performed much the same way as addition and subtraction, but instead by multiplying the corresponding coefficients. If 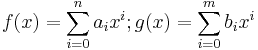 then multiplication is defined as
then multiplication is defined as 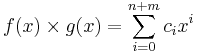 where
where 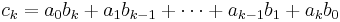 . Note that we treat
. Note that we treat 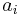 as zero for
as zero for 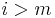 and that the degree of the product is equal to the sum of the degrees to the two polynomials.
and that the degree of the product is equal to the sum of the degrees to the two polynomials.
References
- Stallings, William; : "Cryptography And Network Security: Principles and Practice", pages 121-126. Prentice Hall, 1999.